library(ggdag)
Attaching package: 'ggdag'The following object is masked from 'package:stats':
filterdag1_confound_ggdag <- dagify(
C ~ A + B
)
# Plot the DAG
ggdag(dag1_confound_ggdag) + theme_dag_blank()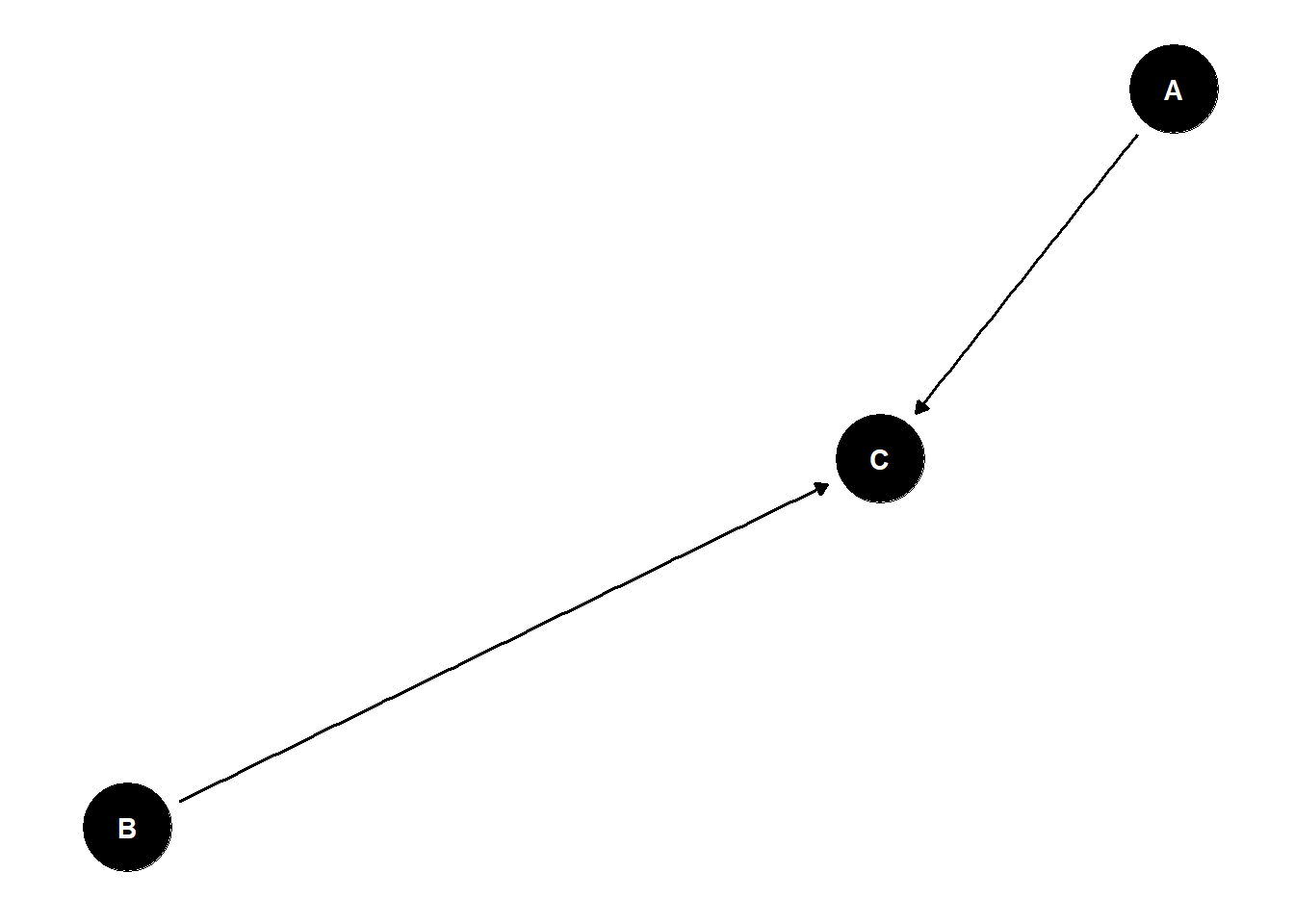
Two variables are said to be d-separated if all paths between them are blocked (otherwise they are d-connected). Two sets of variables are said to be d-separated if each variable in the first set is d-separated from every variable in the second set.
1. If there are no variables being conditioned on, a path is blocked if and only if two arrowheads on the path collide at some variable on the path.
library(ggdag)
Attaching package: 'ggdag'The following object is masked from 'package:stats':
filterdag1_confound_ggdag <- dagify(
C ~ A + B
)
# Plot the DAG
ggdag(dag1_confound_ggdag) + theme_dag_blank()
D=Drivingskills
A=Alkohol
U=Unfall
Der Pfad zwischen den Drivingskills und dem Alkoholkonsum ist durch den Collider Unfall blockiert.
dag2_confound_ggdag <- dagify(
U ~ D + A
)
# Plot the DAG
ggdag(dag2_confound_ggdag, layout = "circle") + theme_dag_blank()
# set number of observations
n <- 10000
D <- rnorm(n, 0, 1)
A <- rbinom(n, 1, 0.05)
U <- 0.01 + 0.3*A - 0.1 * D + rnorm(n, 0, 1)
lm(U ~ A + D)
Call:
lm(formula = U ~ A + D)
Coefficients:
(Intercept) A D
0.02153 0.29753 -0.09725 2. Any path that contains a noncollider that has been conditioned on is blocked.
The path between A and C is blocked, conditioning on B.
dag3_confound_ggdag <- dagify(
C ~ B,
B ~ A,
coords = list(x = c(A = 1, B = 2, C = 3),
y = c(A = 1, B = 1, C = 1))
)
# Plot the DAG
ggdag(dag3_confound_ggdag) + theme_dag_blank()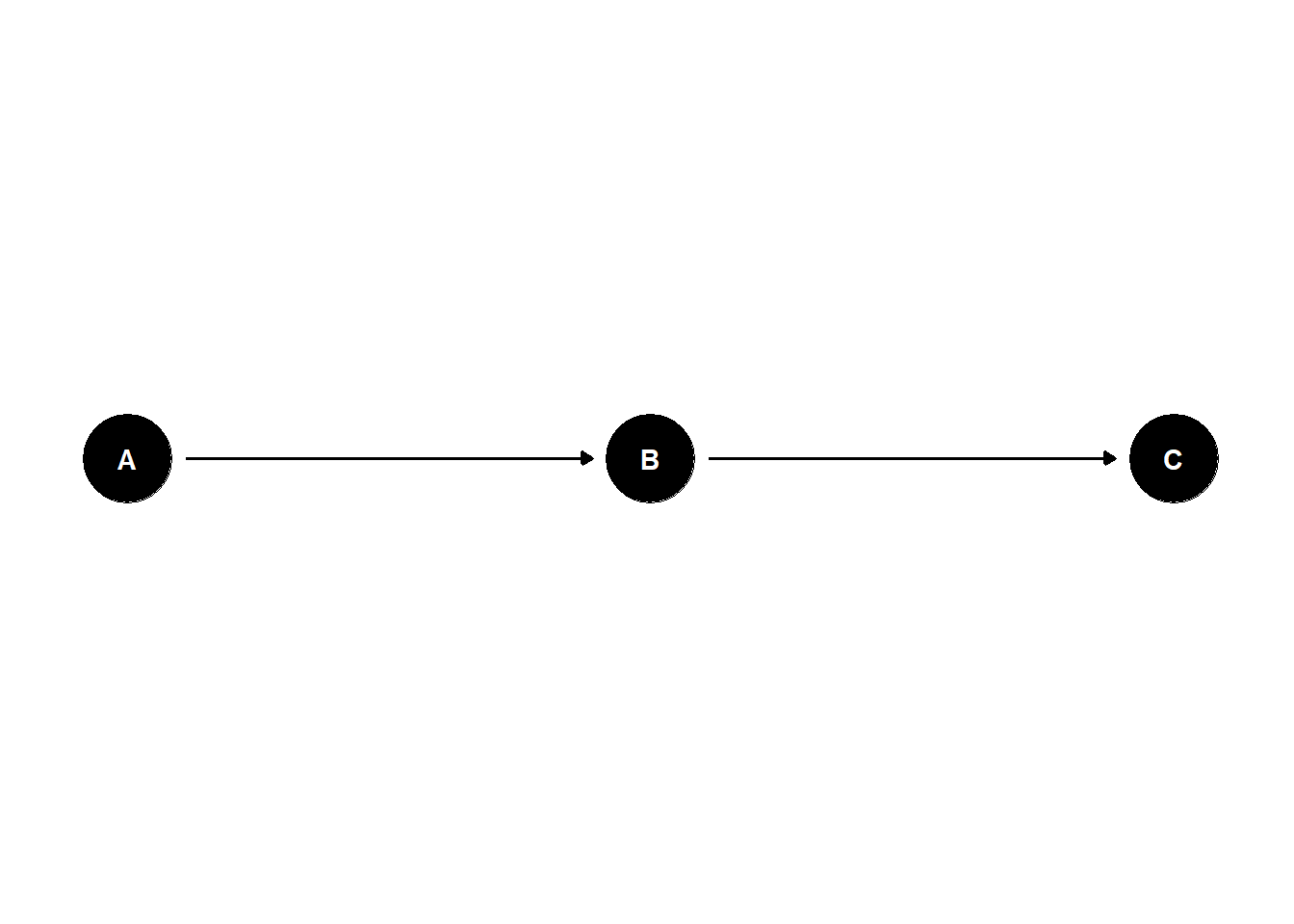
F=Feuer
R=Rauch
A=Alarm
Feuer und Alarm sind unabhängig, bedingt auf Rauch.
dag4_confound_ggdag <- dagify(
A ~ R,
R ~ F,
coords = list(x = c(F = 1, R = 2, A = 3),
y = c(F = 1, R = 1, A = 1))
)
# Plot the DAG
ggdag(dag4_confound_ggdag) + theme_dag_blank()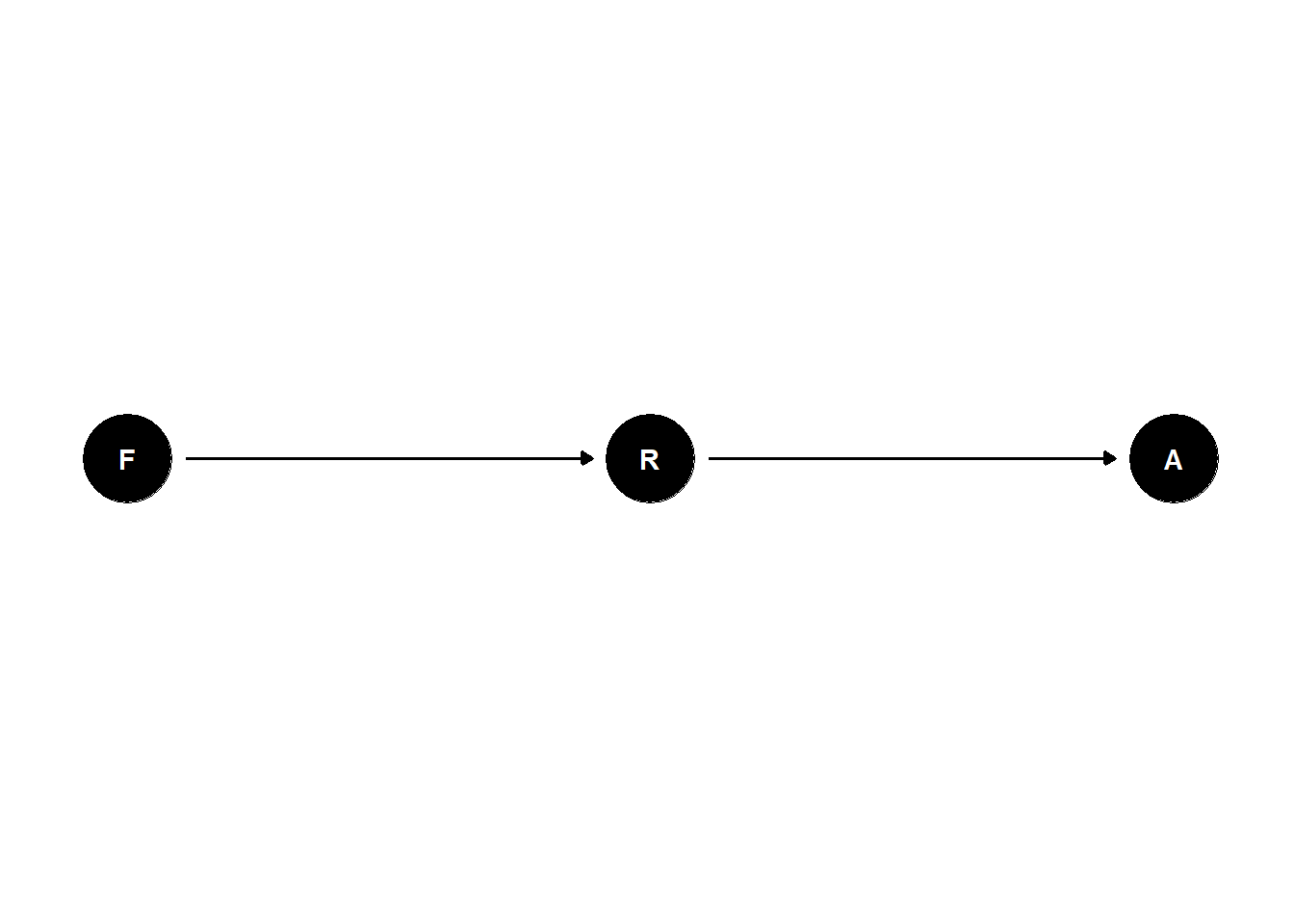
3. A collider that has been conditioned on does not block a path. If we condition on C, the path between A and B is not blocked. They are d-connected.
dag5_confound_ggdag <- dagify(
C ~ A + B
)
# Plot the DAG
ggdag(dag5_confound_ggdag, layout = "circle") + theme_dag_blank()
Durch die Konditionierung auf “Unfall” ist der Pfad zwischen Drivingskills und Alkohol nicht mehr blockiert.
dag6_confound_ggdag <- dagify(
U ~ D + A
)
# Plot the DAG
ggdag(dag6_confound_ggdag, layout = "circle") + theme_dag_blank()
4. A collider that has a descendant that has been conditioned on does not block a path.
library(ggdag)
dag7_confound_ggdag <- dagify(
C ~ A + B,
D ~C,
coords = list(x = c(B = 1, C = 2, D = 2, A = 3),
y = c(B = 3, C = 2, D = 1, A = 3))
)
# Plot the DAG
ggdag(dag7_confound_ggdag) + theme_dag_blank()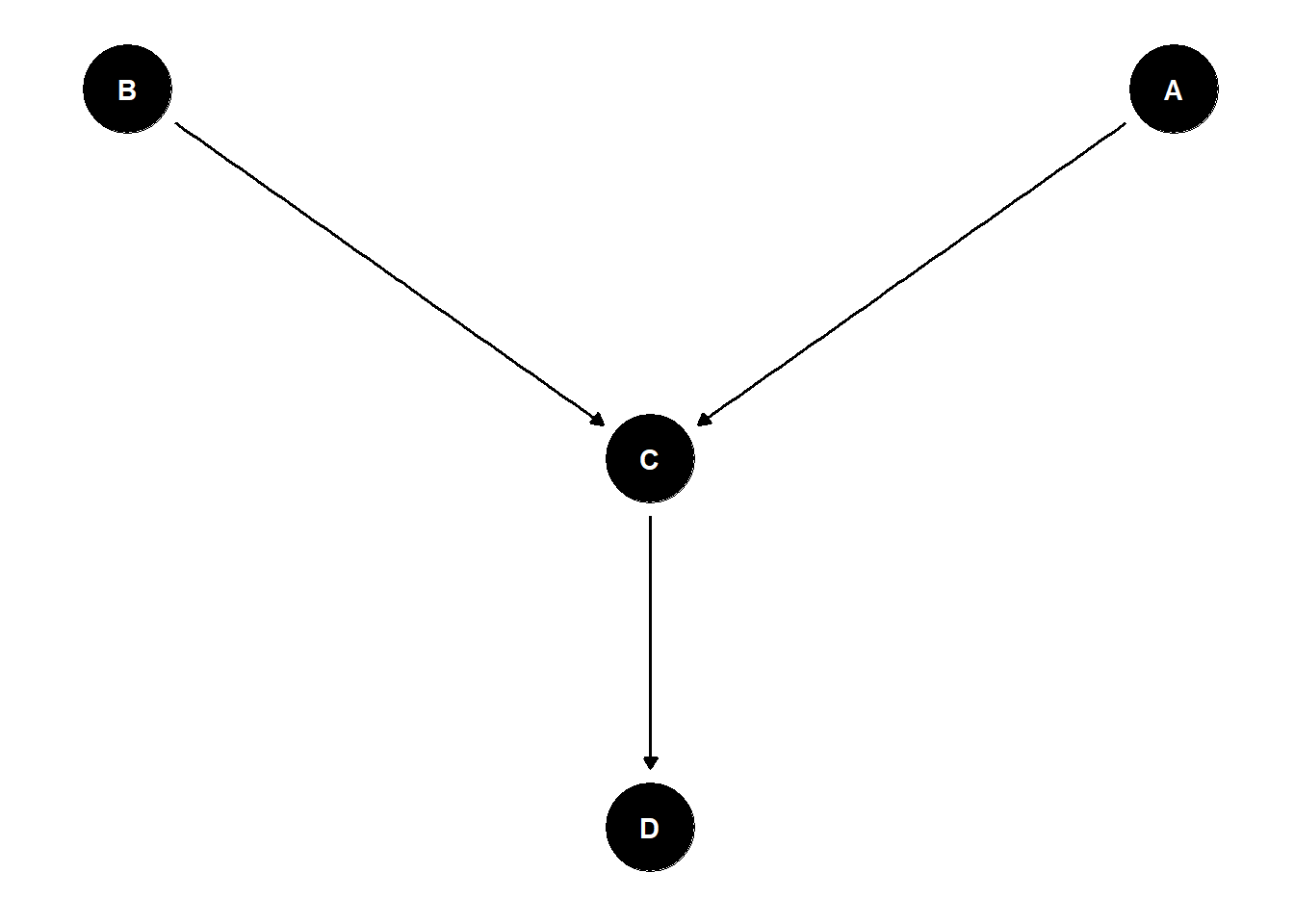
Neue Variable S=Schäden am Auto
Die Variable “Schäden am Auto” ist ein Nachfolger des Colliders “Unfall”. D und A waren d-seperated durch Collider U, aber sind d-connected, sobald wir auf S bedingen.
library(ggdag)
dag8_confound_ggdag <- dagify(
U ~ D + A,
S ~ U,
coords = list(x = c(D = 1, U = 2, S = 2, A = 3),
y = c(D = 3, U = 2, S = 1, A = 3))
)
# Plot the DAG
ggdag(dag8_confound_ggdag) + theme_dag_blank()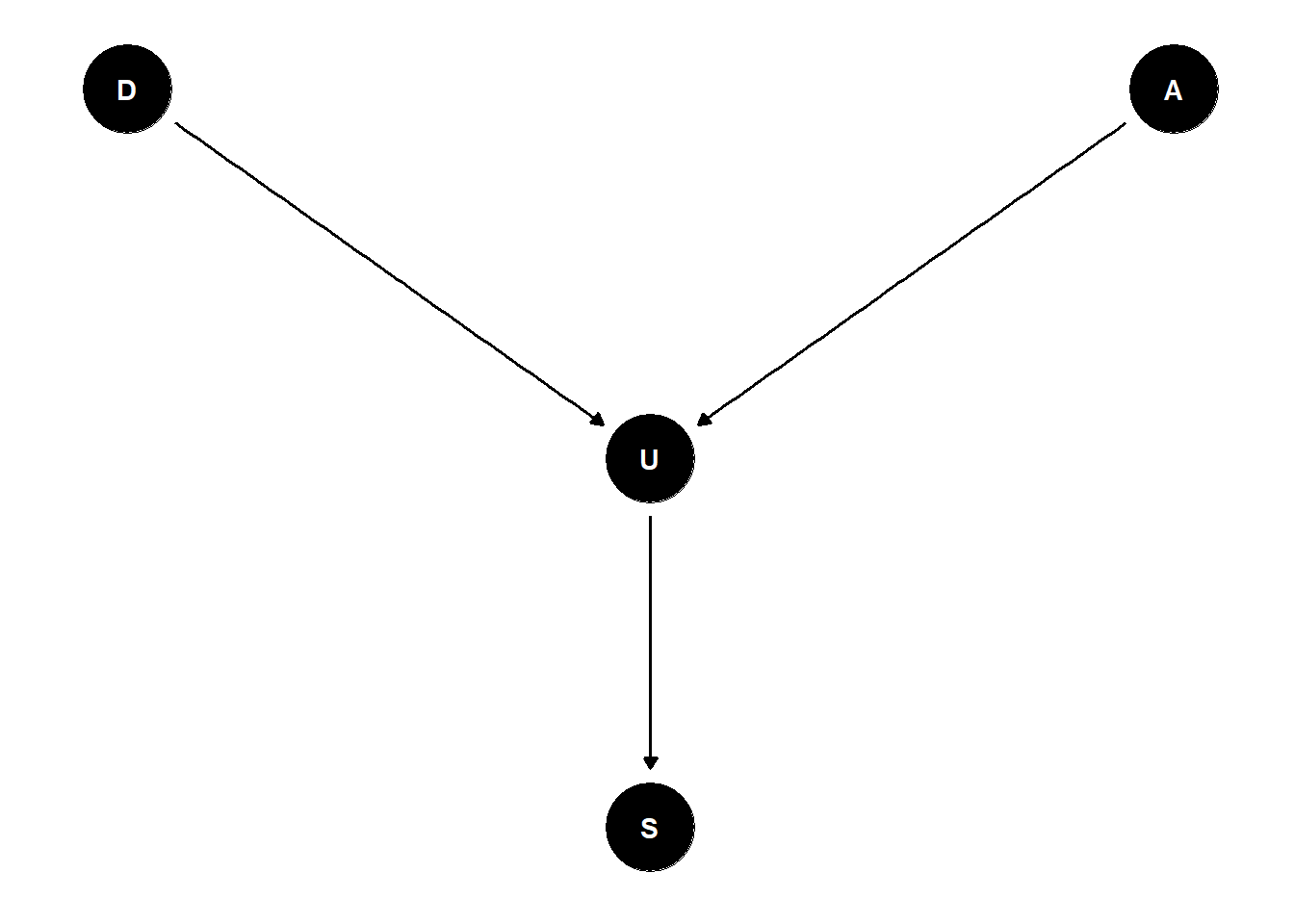
What sets of variables d-seperate the nonadjacent nodes in this DAG?
dag9_confound_ggdag <- dagify(
X ~ Z1 + Z3,
Z3 ~ Z1 + Z2,
W ~ X,
Y ~ W + Z2 + Z3,
coords = list(x = c(X = 1, Z1 = 1, Z3 = 2, W = 2, Z2 = 3, Y = 3),
y = c(X = 1, Z1 = 3, Z3 = 2, W = 1, Z2 = 3, Y = 1))
)
# Plot the DAG
ggdag(dag9_confound_ggdag) + theme_dag_blank()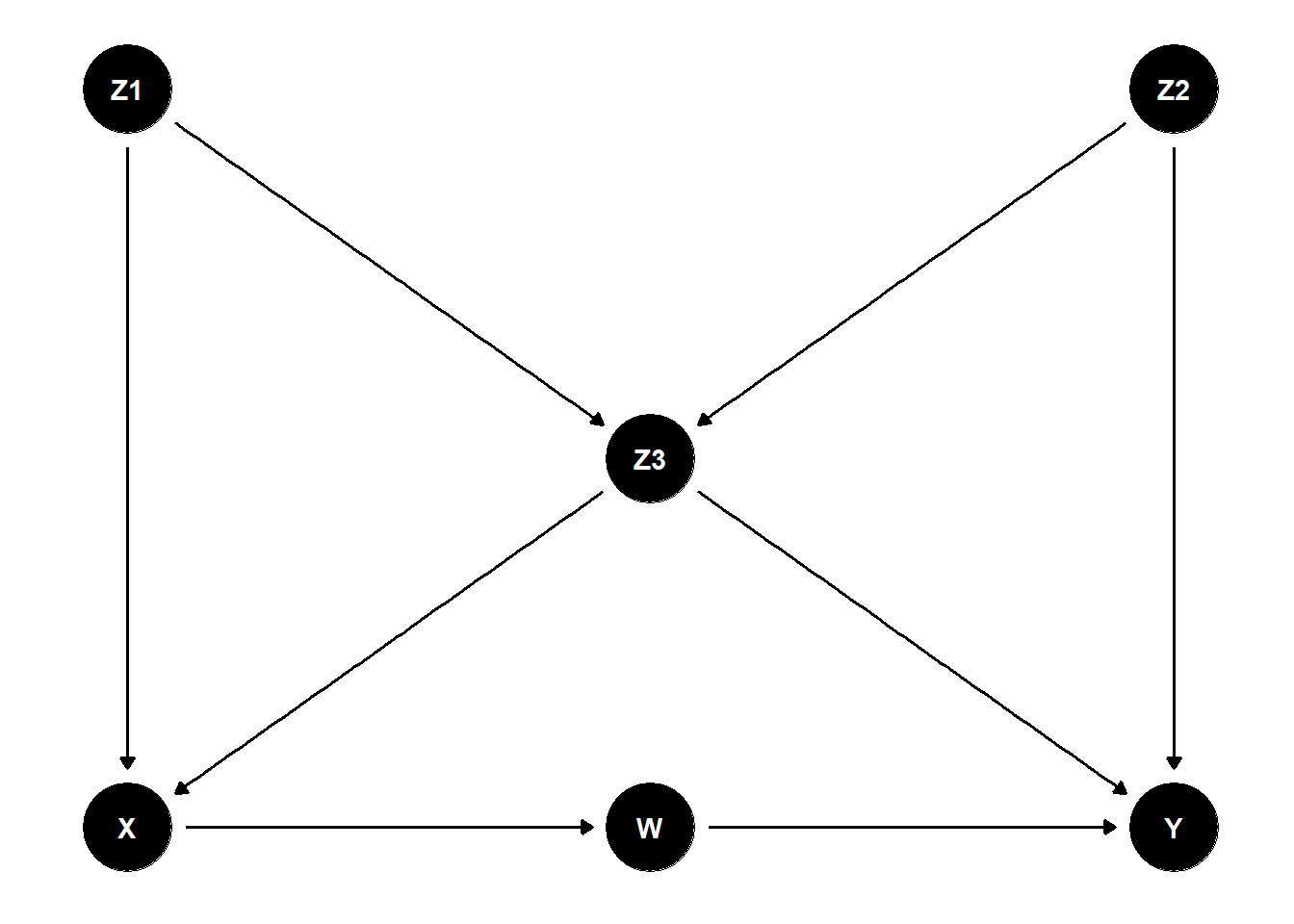
Z1 ⊥⊥ Z2
X ⊥⊥ Y | W, Z3, Z1
oder
X ⊥⊥ Y | W, Z2, Z3
X ⊥⊥ Y | Z1, Z3
W ⊥⊥ Z2 | Z1, Z3
W ⊥⊥ Z2 | X
W ⊥⊥ Z3 | X
W ⊥⊥ Z1 | X
Z1 ⊥⊥ Y |Z3, X, Z2
oder
Z1 ⊥⊥ Y | Z3, W, Z2